Visual-Inertial Relative Pose Estimation for Quadrotor Landing
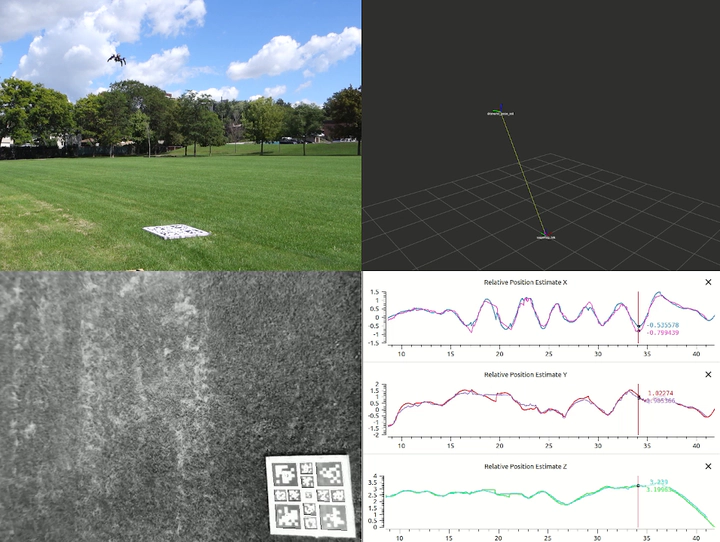
This was my final project at UTIAS where I developed a visual-inertial estimation algorithm for estimating the relative pose of a quadrotor over a landing pad and deployed it on a custom hardware platform.
Overview
This work was performed as part of an overarching personal project to build a quadrotor from hobby grade components capable of autonomously taking off, flying to a target GPS location and then executing a precision landing on a landing pad at that location. One of the most crucial aspects of this system is deriving an accurate estimate of the vehicle relative pose for control of the final landing phase. Low cost GPS units typically only achieve horizontal position accuracies on the order of 2.5 m [1], which is good for general purpose or return to launch flight but insufficient for a precise landing.
More accurate measurements of the relative pose can be achieved via vision with an onboard camera, which has been well explored in the literature [2][3]. These pose measurements can then be fused with IMU data to achieve a high rate state estimate. Thus for this project I investigated developing a visual-inertial estimation algorithm for implementation on a low cost quadrotor.
Approach
Filter Architecture and Software Implementation
To simplify the vision problem I placed an AprilTag fiducial marker on the landing pad, which are commonly used in robotics and allow the full 6 DoF pose to be estimated with a monocular camera [4]. The picture below shows the overall estimation problem and coordinate frames involved.
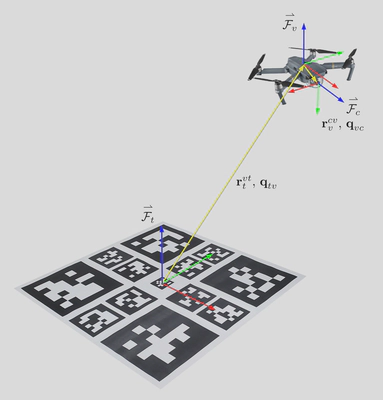
I used a Multiplicative Extended Kalman Filter [5] to estimate both the relative pose and the IMU biases. This framework breaks the state up into a nominal and perturbation component that allows the attitude quaternion to be estimated with a conventional Kalman Filter, which is normally limited to vector spaces. The full details of the derivation are available in the report.
I implemented the filter in a C++ ROS node, which takes IMU data and the pose of the tag from the AprilTag ROS node [6] as inputs and outputs the estimated relative pose and covariance. Due to the cost of the image processing pipeline, the detections reach the filter with a significant delay, which was on the order of 0.2 s in the hardware setup. For this reason the tag detections are fused to a past state based on the estimated delay.
Hardware Platform
The filter was deployed on a custom quadrotor platform illustrated below. Flight control is performed by a Holybro Kakute F7 flight controller running ArduPilot 4.2.2 and the filter runs on a NVIDIA Jetson Nano 4GB using images from an industrial machine vision camera. The vehicle has a total mass of 1.115 kg and estimated maximum thrust of 36.9 N based on data from the motor manufacturer, leading to a thrust to weight ratio of 3.4.

To make the image processing time tractable, the camera image is downsampled to 640x480 to allow the AprilTag node to produce detections at 15 Hz. A custom landing target was designed using a bundle of 13 AprilTags of different sizes within a 0.84 m wide square, which allows for some tags to remain visible when the vehicle is offset laterally.

Validation
Simulation
The filter was first validated in simulation using the TRAILab fork of the RotorS simulator [7] before testing in hardware. The flight was simulated using prerecorded open loop transmitter inputs for manual sweeping flights over the AprilTag target at heights of 2 m and 4 m. The video below for the 2 m case shows the estimated and ground truth pose visualized with RViz as well as the simulated camera view with the AprilTag detection overlaid.
The filter generally tracks the ground truth position and orientation well, with estimation errors below approximately 0.050 m as long as detection is maintained. The cameras loses sight of the tag multiple times during the run at the edges of its sweeping trajectory, leading to drift in the state estimate. In this example we at one point observe a drift of 0.58 m in the position estimate after 5 s of lost detection around 50 s into the event. While not ideal, this is a relatively long interval to go without correction from measurements.
Additional details of the orientation estimate and filter consistency are available in the report.
Hardware Testing
The filter was then validated via outdoor flight tests on the quadrotor platform under manual flight. Two cases were evaluated, including a sweeping flight back and forth over the target as well as a full landing. The height in the sweeping flight case was approximately 2.5 m while the landing case began from a height of approximately 5 m.
The videos below show ground and onboard camera views along with the RViz visualization of the state estimate and time traces for both cases.
$$ $$
No ground truth is available so the estimate is instead compared against the AprilTag reported pose for reference. While detection is maintained the filter does a good job of tracking the magnitude of the motions observed visually. The filter rejects noise in the reported pose at higher heights and exhibits a phase lead relative to the reported pose due to the delay compensation.
The camera loses sight of the tag when changing directions at the edge of its trajectory, leading to drift in the estimate. A maximum drift of approximately 0.71 m is seen around 19 s into the event. Drift also occurs after touchdown when view of the tag is lost that would need to be disabled by the overall state machine when implemented in the full system.
The filter was additionally evaluated indoors when moving the vehicle around by hand, the results of which are summarized in the report.
Challenges
A number of challenges were encountered through development that currently limit performance of the filter:
- The delay in the pose measurements significantly affects filter performance as the pose drives what state the IMU prediction propagates from
- Exact capture time is uncertain due to camera not supporting software trigger. Delay is currently estimated via approximate time stamp plus a constant offset
- The AprilTag detector has a tendency to produce spurious rotation estimates when a tag in the bundle is close to the edge of the image
- Tag can be detected when not fully in image, but are clipped to lie in image skewing the orientation
- Drift in the estimate on lost detections remains a challenge and is negatively influenced by both of the above issues
- The lack of orientation feedback under lost detections leads orientation errors to produce an acceleration bias due to gravity
- Visibility of the tag under bright sunlight, leading to lost detections at higher heights even when the tag is fully in view
Conclusions and Future Work
Despite these challenges, I still managed to produce a visual-inertial filter capable of achieving good estimation performance as long as detections are maintained. The performance is sufficient to deploy with a relative position controller and state machine for executing relative motions and landing maneuvers under nominal conditions, which is the next phase of the project.
Some of the future work for improved performance includes:
- Add additional measurements to improve robustness to lost detections. Possible options:
- Orientation reference, potentially from a simpler IMU only method such as the Mahony filter [8]
- Barometer to provide height feedback
- Motor thrust model, allows moving accelerometer data to measurement side of the EKF
- Update to a more advanced filter architecture such as a Sigma Point or Iterated Extended Kalman Filter
- Improve rejection of spurious AprilTag orientation estimates
- Explore a GPU implementation of AprilTag detector to potentially reduce need for downsampling, increase run rate or reduce delay time
References
[1] u-blox SAM-M8Q Data Sheet
[2] K. Ling, D. Chow, A. Das, and S. L. Waslander, “Autonomous maritime landings for low-cost VTOL aerial vehicles,” in 2014 Canadian Conference on Computer and Robot Vision, pp. 32–39, 2014.
[3] A. Paris, B. T. Lopez, and J. P. How, “Dynamic landing of an autonomous quadrotor on a moving platform in turbulent wind conditions.” https://arxiv.org/abs/1909.11071, 2019.
[4] M. Krogius, A. Haggenmiller, and E. Olson, “Flexible Layouts for Fiducial Tags,” in 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 1898–1903, 2019.
[5] F. L. Markley, “Attitude Error Representations for Kalman Filtering,” Journal of Guidance, Control, and Dynamics, vol. 26, no. 2, pp. 311–317, 2003.
[6] D. Malyuta, C. Brommer, D. Hentzen, T. Stastny, R. Siegwart, and R. Brockers, “Long-duration fully autonomous operation of rotorcraft unmanned aerial systems for remote-sensing data acquisition,” Journal of Field Robotics, p. arXiv:1908.06381, Aug. 2019.
[7] F. Furrer, M. Burri, M. Achtelik, and R. Siegwart, Robot Operating System (ROS): The Complete Reference (Volume 1), ch. RotorS—A Modular Gazebo MAV Simulator Framework, pp. 595–625. Cham: Springer International Publishing, 2016.
[8] R. Mahony, T. Hamel, and J.-M. Pflimlin, “Nonlinear complementary filters on the special orthogonal group,” IEEE Transactions on Automatic Control, vol. 53, no. 5, pp. 1203–1218, 2008.